
Return to story index
e-mail author (edward@ordman.net)
Author Info
Is Sudoku Mathematics? (Is composing mazes mathematics?)
An essay in the Monitor in October 2005, commenting
on the new Sudoku puzzles, asserts they require no mathematics
skills. I concede that they require no arithmetic, but the
logical reasoning that they require is certainly mathematics.
During a career as a college professor of mathematics, I enjoyed
distinguishing between math and arithmetic, even when guest lecturing
to, for example, nine-year-olds.
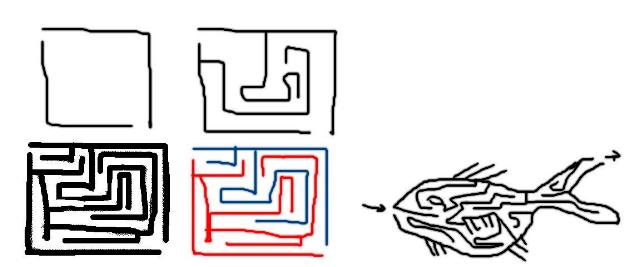
Let me offer a simple example: here is
a method for constructing mazes. As a child, I loved mazes,
but couldn’t make one myself without drawing the answer first and then
drawing the maze around the answer - not very satisfactory, as the
answer was then already filled in! I didn’t realize the essential
trick until graduate school. Take a paper and two colored pencils
(or a pencil and pen) and follow along.
Draw a rectangular box (with the pen if
you have one), with the upper left corner open for an entrance and the
lower right open for an exit. Now add lines to the maze as
follows: you can put in any sort of a line you want - straight, curved,
turning corners - provided that each line you add touches exactly one
line that was there already. (It cannot touch zero, it cannot
touch two.)
<<Incidentally, the maze need not be a rectangle - see the
diagram below.>>
When you have the box full enough with lines,
stop. I claim that the result is a maze - maybe an easy one,
maybe a hard one. It has exactly one solution - one path through
from the start to the finish.
Why am I sure there is a solution,
and just one solution? Let’s draw the maze again, using two
colors this time (we’ll call them blue and red, but any two
colors - or a pen and pencil - will do.) When you draw the
box, make the top and right edges blue, and the bottom and left edges
red (so you have one blue line, with a corner, and one red
line, with a corner.) Now when you add new lines to the drawing,
each new line touches exactly one old line - make it the same color as
the line it touches. The red and blue parts of the picture grow
like spiders or tangles of spaghetti , getting tangled together, but
there are always two parts, a red part and a blue part. And when you
are done, there is one path through the maze - just start at the
beginning and keep the blue on your left and the red on your right, and
you’ll find the path through!
This is clearly mathematics - it
depends critically on the difference between “two” and “not two.”
But it is not arithmetic (and neither is Sudoku.)
I’ve had a class go out to the
playground at recess, teach this to the class next door, and have that
class go in and show it to their teacher and convince the second
teacher that the method works. But I didn’t let on that they were
reproducing a “theorem” and a “proof,” which I suspect might have
scared them off. I like mathematics, and suspect some other
people do to - maybe especially if they don’t know if they are doing
mathematics.
Edward Ordman (C) 2005
Back to Story Index
